Mo logo [home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff] german flag
Mathematics-Online course: Linear Algebra - Analytic Geometry - Orthogonal Groups

Rotation Axis and Angle

[previous page] [next page] [table of contents][page overview]
A rotation $ Q$ in $ \mathbb{R}^3$ has an axis of rotation, i.e. $ Q$ fixes an unit vector $ u$, and corresponds to a plane rotation by an angle $ \vartheta$ in the plane orthogonal to $ u$.

With respect to an orthonormal right-handed coordinate system $ u,v,w$, the matrix representation of $ Q$ is given by:

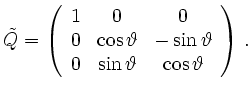
$\displaystyle \tilde Q = \left(\begin{array}{ccc} 1&0&0 \\ 0&\cos\vartheta & -\sin\vartheta \\ 0&\sin\vartheta & \cos\vartheta \\ \end{array}\right) \,. $

For the angle of rotation

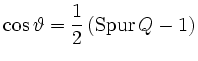
$\displaystyle \cos\vartheta = \frac{1}{2}\left(\operatorname{Spur} Q - 1\right) $

holds.
(Authors: Höllig/Reble/Höfert)
(temporary unavailable)
With the rotation-matrix

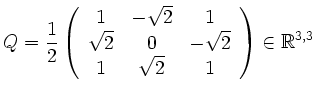
$\displaystyle Q = \frac{1}{2} \left( \begin{array}{ccc} 1 & -\sqrt{2} & 1 \\ \s... ...& 0 & -\sqrt{2} \\ 1 & \sqrt{2} & 1 \end{array} \right) \in \mathbb{R}^{3,3} $

you get

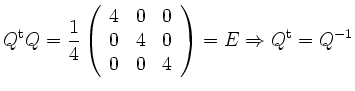
$\displaystyle Q^{\operatorname t}Q = \frac{1}{4} \left( \begin{array}{ccc} 4 & ... ...\\ 0 & 0 & 4 \end{array} \right) = E \Rightarrow Q^{\operatorname t}= Q^{-1} $

and

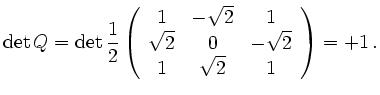
$\displaystyle \operatorname{det} Q = \operatorname{det} \frac{1}{2} \left( \beg... ...\ \sqrt{2} & 0 & -\sqrt{2} \\ 1 & \sqrt{2} & 1 \end{array} \right) = + 1\,. $

Compute the rotationaxis, the eigenvector $ v$ to the eigenvalue $ \lambda = 1$:

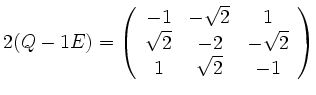
$\displaystyle 2(Q-1E) = \left( \begin{array}{ccc} -1 & -\sqrt{2} & 1 \\ \sqrt{2} & -2 & -\sqrt{2} \\ 1 & \sqrt{2} & -1 \end{array} \right) $

With 2nd row $ - \sqrt{2} \cdot$ 1st row and 3rd row $ +$ 1st row you get

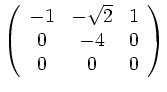
$\displaystyle \left( \begin{array}{ccc} -1 & -\sqrt{2} & 1 \\ 0 & -4 & 0 \\ 0 & 0 & 0 \end{array} \right) $

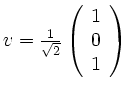and so the eigenvector $ v = \frac{1}{\sqrt{2}} \left( \begin{array}{c} 1 \\ 0 \\ 1 \end{array} \right)$.

To compute $ \varphi$ you compute the angle between an unit vector $ n$ with $ n \bot v$ and the unit vector $ x = Qn$.

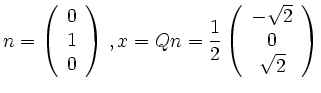
$\displaystyle n = \left( \begin{array}{c} 0 \\ 1 \\ 0 \end{array} \right)\,, x... ...{1}{2} \left( \begin{array}{c} -\sqrt{2} \\ 0 \\ \sqrt{2} \end{array} \right) $

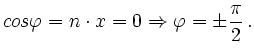
$\displaystyle cos \varphi = n \cdot x = 0 \Rightarrow \varphi = \pm \frac{\pi}{2}\,. $

  automatically generated 4/21/2005