Mo logo [home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff] german flag
Mathematics-Online course: Linear Algebra - Normal Forms - Jordan Normal Form

Cyclic Bases of Generalized Eigenspaces

[previous page] [next page] [table of contents][page overview]
A generalised eigenspace of a matrix $ A$ can be decomposed in a direct sum of cyclic subspaces:

$\displaystyle H_\lambda = V_1 \oplus \cdots \oplus V_\ell\,, $

that is, each subspace $ V_i$ has a basis of the form

$\displaystyle B^{k_i}v_i,\,\ldots,\,Bv_i,\,v_i, \quad B=A-\lambda E, $

where $ w_i = B^{k_i}v_i$ is a eigenvector for eigenvalue $ \lambda$.

The subspaces $ V_i$ are invariant under matrix $ A$. The restriction of $ A$ onto these subspaces has the representation:

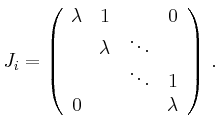
$\displaystyle J_i = \left(\begin{array}{cccc} \lambda & 1 & & 0 \\ & \lambda & \ddots \\ & & \ddots & 1 \\ 0 & & & \lambda \end{array}\right) \,. $

By definition, $ H_\lambda$ consists of vectors $ v$ with $ B^{k+1} v=0$, where $ k$ is smaller than the algebraic multiplicity $ m$ of $ \lambda$. Therefore we chose a basis of this special form. In order to find the vectors

$\displaystyle w_i \in \operatorname{ker}B $

forming a basis, we consider the subspaces

$\displaystyle U_j = \operatorname{ker}B\,\cap\,\operatorname{Im}B^j $

of the eigenspace $ \operatorname{ker}B$ for $ \lambda$. Obviously we have

$\displaystyle \emptyset = U_m \subset U_{m-1} \subset \cdots \subset U_0 = \operatorname{ker}B \,. $

Starting from the empty set the vectors $ w_i$ are constructed inductively. If $ w_1,\ldots,w_{i-1}$ are already determined, then find the maximal $ k_i$ so that $ U_{k_i}$ does not lie in the linear hull $ W_{i-1}$ of $ w_j$, that is, there is $ v_i\ne0$ with

$\displaystyle B^{k_i} v_i = w_i\notin W_{i-1},\quad Bw_i = 0\,. $

That way we find a basis $ \{w_1,\ldots,w_\ell\}$ for the whole eigenspace $ \operatorname{ker}B$ and we find respective cyclic bases for the spaces $ V_i$.

The invariance of the spaces $ V_i$ under multiplication by $ B$ (or $ A$, resp.) is obvious. The asserted matrix representation of $ A$ on $ V_i$ follows from

$\displaystyle A (B^j v_i) = (\lambda E + B) B^j v_i = \lambda B^j v_i + B^{j+1} v_i \,, $

ordering the basis vectors by descending powers.

It remains to be proved that the vectors $ B^j v_i$ form a basis. This will be shown in two steps.

(i) At first we show the linear independence. The example of two cyclic chains

$\displaystyle B^2 v_1,\, Bv_1,\, v_1,\quad Bv_2,\, v_2\,, $

illustrates the rather technical argument. Supposing that

$\displaystyle \alpha_{2,1}B^2 v_1+\alpha_{1,1}Bv_1 + \alpha_{0,1}v_1 + \alpha_{1,2}B v_2+\alpha_{0,2}v_2 = 0, $

it follows from multiplication by $ B^2$

$\displaystyle \alpha_{0,1} w_1 = 0 \implies \alpha_{0,1} = 0 \,, $

since $ B^3 v_1 = Bw_1 = 0$ and $ B^2 v_2 = Bw_2 = 0$. Multiplication by $ B$ yields

$\displaystyle \alpha_{1,1}w_1 + \alpha_{0,2}w_2 = 0 \implies \alpha_{1,1}=\alpha_{0,2}=0 $

since the eigenvectors $ w_i$ are linearly independent by construction. Again it follows from the linear independence of the eigenvectors $ w_i$ that

$\displaystyle \alpha_{2,1}=\alpha_{1,2}=0\,. $

The general case is proved in an analogous way. A linear combination of basis vectors is analysed by multiplying it by appropriate powers of $ B$ in order to nullify all terms except for eigenvectors.

(ii) It remains to be proved that any vector $ u\in H_\lambda$ can be represented by means of the basis vectors. Let

$\displaystyle B^k u = 0\,, $

with $ k\le m$. For $ k=1$ nothing remains to be proved since, by construction, the vectors $ w_i$ form a basis for the eigenspace $ \operatorname{ker}B$. Hence, we can inductively assume that vectors in $ \operatorname{ker}B^{k-1}$ can be represented. $ B^{k-1} u$ can also be represented:

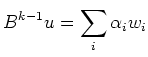
$\displaystyle B^{k-1} u = \sum_i \alpha_i w_i $

where $ w_i\in U_{k-1}$. From this it follows that

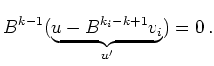
$\displaystyle B^{k-1} (\underbrace{u - B^{k_i-k+1}v_i}_{u'}) = 0 \,. $

Consequently, $ u'$ has a representation and, thus, so does $ u$.

(Authors: Burkhardt/Höllig/Hörner)
  automatically generated 4/21/2005