

Mathematics-Online course: Linear Algebra - Normal Forms - Jordan Normal Form

|
[home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff] |

|
|
Mathematics-Online course: Linear Algebra - Normal Forms - Jordan Normal Form | ||
Generalized Eigenvectors | ||
| [previous page] [next page] | [table of contents][page overview] |
In order to find the dimension we bring matrix ![]() to upper triangle form:
to upper triangle form:
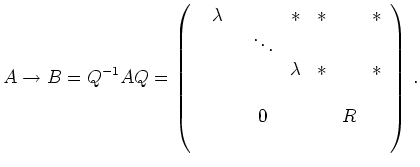
| automatically generated 4/21/2005 |