Mo logo [home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff] german flag
Mathematics-Online course: Preparatory Course Mathematics - Analysis - Differential Calculus

Babylonian Square Root Iteration

[previous page] [next page] [table of contents][page overview]
The iteration

$\displaystyle x \longleftarrow (x+a/x)/2 \,, $

to determine the square root of a positive number $ a$, was already used by the Babylonians. A closer look reveals the equivalence to Newton's method applied to the function $ f(x)=x^2-a$:

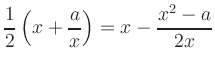
$\displaystyle \frac{1}{2}\left(x+\frac{a}{x}\right)=x-\frac{x^2-a}{2x} $

For $ a=2$ and $ x_0=1$ we obtain the approximations
1
1.5
1.416666666666666666666666666666666666667
1.414215686274509803921568627450980392157
1.414213562374689910626295578890134910117
1.414213562373095048801689623502530243615
1.414213562373095048801688724209698078570

Apparently, the convergence is quite fast. With each step the number of correct digits (underlined) nearly doubles.

In this example, quadratic convergence can be proved directly by a simple algebraic manipulation:

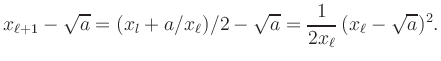
$\displaystyle x_{\ell+1}-\sqrt{a} = (x_l+a/x_\ell)/2-\sqrt{a} = \frac{1}{2x_\ell}\,(x_\ell-\sqrt{a})^2. $

The geometric interpretation of Newton's method shows that the iteration is convergent for any $ x_0 \neq 0$

[previous page] [next page] [table of contents][page overview]
  automatically generated 1/9/2017