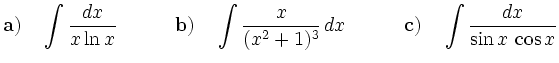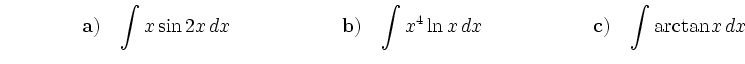[an error occurred while processing this directive]
[an error occurred while processing this directive]
Let the function 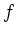 be differentiable at
be differentiable at
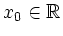 and let
and let
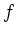 further suffice the equation
further suffice the equation
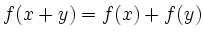 for all
for all
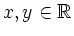 .
.
- a)
- Use the difference quotient to show that
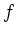 is
differentiable for all
is
differentiable for all
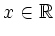 .
.
- b)
- Prove the existence of a constant
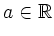 with
with 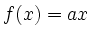 for all
for all
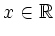 .
.
(Authors: Wipper/Abele)
[an error occurred while processing this directive]
[an error occurred while processing this directive]
The front of a greenhouse shall have the form of a axes-symmetric pentagon with three
right angles (cp.figure). The amount of the glass wall is limited by 20 m; the area
within shall be maximised.
What's the height and the width of the greenhouse?
|
(Authors: Apprich/Höfert)
Given the function
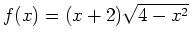 .
.
- a)
- For which
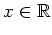
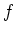 is defined? Check where
is defined? Check where 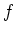 is
differentiable and determine
is
differentiable and determine 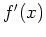 .
.
- b)
- What are the roots and lokal extremums of
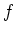 ?
?
- c)
- What's the behaviour of
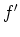 for the boundary of the domain?
for the boundary of the domain?
- d)
- Sketch the graph of
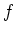 .
.
(Authors: /Höfert)
[an error occurred while processing this directive]
[an error occurred while processing this directive]
Let 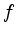 and
and 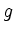 be the real functions given by
be the real functions given by
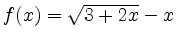 and
and
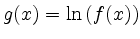 .
.
- a)
- Determine
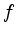 's domain and sketch
the graph. What is
's domain and sketch
the graph. What is 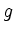 's domain?
's domain?
- b)
- Examine
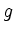 with regard to zero points, asymptotes and local
extrema.
with regard to zero points, asymptotes and local
extrema.
- c)
- How do
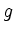 and
and 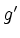 behave at the domain's boundary points?
behave at the domain's boundary points?
- d)
- Draw the graph of the function
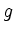 . note:
. note:
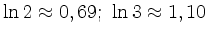 .
.
(Authors: Kimmerle/Roggenkamp/Rump/Abele)
[an error occurred while processing this directive]
[an error occurred while processing this directive]
[an error occurred while processing this directive]
[an error occurred while processing this directive]
[an error occurred while processing this directive]
[an error occurred while processing this directive]
[an error occurred while processing this directive]
[an error occurred while processing this directive]
Use appropriate substitutions to determine the following integrals:
(Authors: Kimmerle/Roggenkamp/Rump/Abele)
Use partial integration to determine the following integrals:
(Authors: Kimmerle/Roggenkamp/Rump/Abele)
| |
automatically generated
1/9/2017 |




![\includegraphics[width=3.5cm]{g25_bild1}](/inhalt/aufgabe/aufgabe120/img1.png)