Check whether the following expressions are tautologies. Use
transcriptions as well as truth tables.
(Authors: Hörner/Lesky/Abele)
The characters
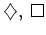 each symbolize one logical
operator of the set
each symbolize one logical
operator of the set
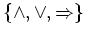 . In which cases
does the following relation hold:
. In which cases
does the following relation hold:
(Authors: Wipper/Abele)
Given are sets
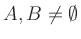 , a map
, a map
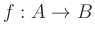 as well
as the subsets
as well
as the subsets
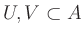 and
and
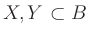 . Consider the
following relations; either prove them or find a suitable
counter-example respectively.
. Consider the
following relations; either prove them or find a suitable
counter-example respectively.
(Authors: Wipper/Abele)
Express the following statements about a map
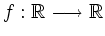 in
the formal way:
in
the formal way:
| a) |
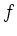 is not
surjective
is not
surjective |
| b) |
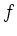 is not injective
is not injective |
| c) |
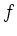 is not bijective
is not bijective |
| d) |
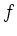 is neither surjective nor injective
is neither surjective nor injective |
(Authors: Apprich/Höfert)
Use induction to proof for
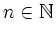 :
:
a)
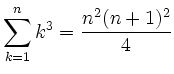
|
| b)
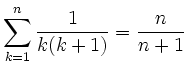
|
(Authors: Kimmerle/Roggenkamp/Höfert)
Prove via mathematical induction for
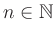 :
:
- a)
-
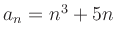 can be divided by
can be divided by 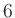 .
.
- b)
-
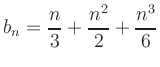 is a natural number.
is a natural number.
(Authors: Boßle/Wipper/Abele)
How many possibilites do exist to express
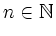 as a sum
of
as a sum
of 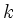 natural numbers, if the order of summands is taken into
account?
natural numbers, if the order of summands is taken into
account?
(Authors: Höllig/Abele)
[an error occurred while processing this directive]
[an error occurred while processing this directive]
[an error occurred while processing this directive]
[an error occurred while processing this directive]
| |
automatically generated
1/9/2017 |




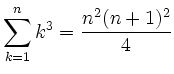
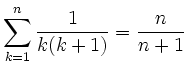
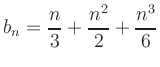 is a natural number.
is a natural number.