Mo logo [home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff] german flag
Mathematics-Online course: Preparatory Course Mathematics - Basics - Complex Numbers

Division of Complex Numbers

[previous page] [next page] [table of contents][page overview]
The quotient $ z_1/z_2$ of two complex numbers

$\displaystyle z_k = x_k + \mathrm{i} y_k = r_k \exp(\mathrm{i}\varphi_k) $

is

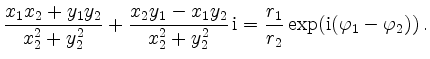
$\displaystyle \frac{x_1x_2+y_1y_2}{x_2^2+y_2^2} + \frac{x_2y_1-x_1y_2}{x_2^2+y_2^2}\,\mathrm{i} = \frac{r_1}{r_2}\exp(\mathrm{i}(\varphi_1-\varphi_2))\, . $

In particular,

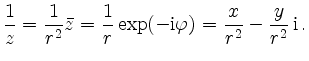
$\displaystyle \frac{1}{z} = \frac{1}{r^2} \bar z = \frac{1}{r} \exp(-\mathrm{i}\varphi) = \frac{x}{r^2} - \frac{y}{r^2}\,\mathrm{i} \,. $

A complex number's reciprocal can be constructed via reflection at the unit circle $ C$, as is illustrated in the following figure.

\includegraphics[height=6cm]{a_division_bild}

The complex conjugate $ w = \bar z$ is the intersection of the diagonals of the quadrilateral formed by the tangents at $ C$ passing through $ z$ and the perpendicular radii. The number $ z$ is then obtained by reflection at the real axis.

(Authors: Höllig/Kopf/Abele)

(temporary unavailable)
(temporary unavailable)
[previous page] [next page] [table of contents][page overview]
  automatically generated 1/9/2017