Mo logo [home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff] german flag
Mathematics-Online course: Preparatory Course Mathematics - Basics - Combinatorics

Binomial Coefficient

[previous page] [next page] [table of contents][page overview]

For $ n,k \in{\mathbb{N}}_0$ with $ n \geq k$ the binomial coefficient $ \binom{n}{k} $ is defined as

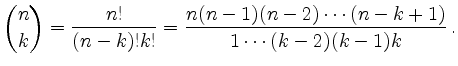
$\displaystyle \binom{n}{k} = \frac{n!}{(n-k)!k!} = \frac{n(n-1)(n-2)\cdots(n-k+1)}{1 \cdots (k-2)(k-1)k}\,. $

With $ 0! = 1$ we have in particular

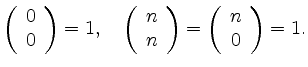
$\displaystyle \left(\begin{array}{c}0 \\ 0\end{array} \right) = 1, \quad \left... ...\ n\end{array} \right) = \left(\begin{array}{c}n \\ 0\end{array}\right) = 1 . $

The binomial coefficient $ \binom{n}{k} $ equals the number of $ k$-subsets of a set containing $ n$ elements.

(Authors: Kimmerle/Abele)
[previous page] [next page] [table of contents][page overview]
  automatically generated 1/9/2017