Mo logo [home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff] german flag
Mathematics-Online course: Preparatory Course Mathematics - Linear Algebra and Geometry - Vector spaces

Basis

[previous page] [next page] [table of contents][page overview]
A subset $ B$ of vector space $ V$ is called basis of $ V$, if $ B$ is linearly independent as well as a generating system for $ V$, that is, any vector $ v\in V$ has a unique representation as finite linear combination

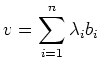
$\displaystyle v = \sum_{i=1}^n \lambda_i b_i $

where $ b_i\in B$.

In a finite-dimensional vector space any vector can be described by its coordinates relative to a given basis:

$\displaystyle v_B = (\lambda_1,\ldots,\lambda_n)^{\operatorname t}\,. $

In an infinite-dimensional vectorspace a generating system $ S$ is a basis if and only if any finite subset of $ S$ consists of linearly independent vectors.

(Authors: App/Burkhardt/Höllig/Kimmerle)

(temporary unavailable)
[previous page] [next page] [table of contents][page overview]
  automatically generated 1/9/2017