Mathematics-Online course: Preparatory Course Mathematics-Linear Algebra and Geometry-Systems of Linear Equations-Gauss Elimination for an invertible Matrix

	[home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff]
	Mathematics-Online course: Preparatory Course Mathematics - Linear Algebra and Geometry - Systems of Linear Equations
	Gauss Elimination for an invertible Matrix

[previous page] [next page]

[table of contents][page overview]

By Gaussian elimination any LSE with invertible $n\times n$ coefficient matrix

can be brought to upper triangular form in at most

steps. For this purpose all coefficients below the diagonal are successively nullified, that is, after $\ell-1$ steps the LSE has the form

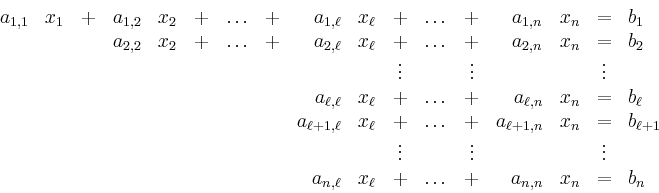
$\begin{displaymath}\begin{array}{rrrrrrrrrrcccrrcl} a_{1,1}&x_1&+&a_{1,2}&x_2&+... ...a_{n,\ell}&x_{\ell}&+&\hdots&+&a_{n,n}&x_n&=&b_n \end{array} \end{displaymath}$

In detail the $\ell$ -th elimination step proceeds as follows:

If the $\ell$ -th diagonal element (the so called pivot element) equals zero, then the $\ell$ -th equation is interchanged with one of the following equations so that $a_{\ell,\ell}\ne0$ .
For an appropriate multiple of the $\ell$ -th equation is subtracted from the -th equation so that $a_{i,\ell}$ equals zero:

$\displaystyle a_{i,j}\leftarrow a_{i,j} - q_i a_{\ell,j},\quad b_i\leftarrow b_i - q_i b_\ell\quad (q_i = a_{i,\ell}/a_{\ell,\ell})\, ,$
where $j\ge\ell$ .

(temporary unavailable)

[previous page] [next page]

[table of contents][page overview]

automatically generated 1/9/2017