

Mathematics-Online course: Vector Calculus - Quadratic Curves

|
[home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff] |

|
|
Mathematics-Online course: Vector Calculus - Quadratic Curves | ||
Rotation of Conic Sections | ||
| [previous page] | [table of contents][page overview] |
If the conic section with the equation
is transformed by a rotation about the origin through the angle ![]() then the equation in the new coordinates
then the equation in the new coordinates ![]() and
and ![]() has the form
has the form
provided
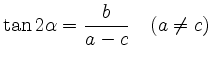
or
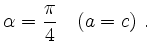
The coordinate transformation which expresses the old coordinates in terms of the new ones is given by
The parameters of the new equation are
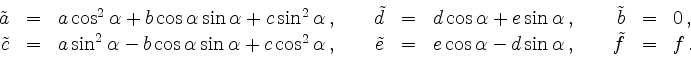
Note that in the new equation there is no mixed quadratic term, i.e. the
coeffcient ![]() of
of
![]() is zero. Thus this equation may be easily further
transformed into a normal form of the conic section by completing squares.
is zero. Thus this equation may be easily further
transformed into a normal form of the conic section by completing squares.
The condition on the angle ![]() of a suitable rotation of the
coordinate axes is
of a suitable rotation of the
coordinate axes is
Thus with
![]()
the coordinate transformation
yields
and the equation gets the form
Consequently the given conic section is a parabola (independent from ![]() ).
).
| [previous page] | [table of contents][page overview] |
| automatically generated 10/30/2007 |