Mo logo [home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff] german flag
Mathematics-Online course: Vector Calculus - Lines

Distance of Two Lines

[previous page] [next page] [table of contents][page overview]
The distance between two lines $ g$ and $ h$ which are not parallel and with parametric equations

$\displaystyle g : \vec{p} + t\vec{u} , t \in \mathbb{R} $

and

$\displaystyle h : \vec{q} + s\vec{v} , s \in \mathbb{R} $

is given by

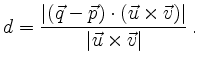
$\displaystyle d = \frac{\vert(\vec{q} - \vec{p}) \cdot (\vec{u} \times \vec{v})\vert} {\vert\vec{u} \times \vec{v}\vert}\, . $

This follows from the geometric properties of the dot and the cross product because the distance coincides with the distance of $ h$ from the plane containing $ g$ and the by $ p-q$ translated line $ h .$

Using the parallelepidial product the distance may be expressed as

$\displaystyle d = \frac{\vert[\overrightarrow{PQ},\vec{u},\vec{v}]\vert} {\vert\vec{u}\times\vec{v}\vert}\, , $

where $ P$ and $ Q$ are the points with location vector $ \vec{p}$ and $ \vec{q}$ rsp.

For parallel lines we have

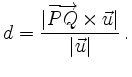
$\displaystyle d = \frac{\vert\overrightarrow{PQ}\times\vec{u}\vert} {\vert\vec{u}\vert}\, . $

\includegraphics[width=11cm]{a_abstand_gerade_gerade_bild}

Two lines are called skew lines if they are not parallel and if the distance between them is positive.

(temporary unavailable)

(temporary unavailable)
[previous page] [next page] [table of contents][page overview]
  automatically generated 10/30/2007