Mo logo [home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff] german flag
Mathematics-Online course: Vector Calculus - Vector Product

Vector Product, Cross Product

[previous page] [next page] [table of contents][page overview]
The vector

$\displaystyle \vec{c} = \vec{a} \times \vec{b} $

is orthogonal to $ \vec{a}$ and $ \vec{b}$. It is oriented by the ,,Right-Hand-Rule`` and has the length

$\displaystyle \bigl\vert\vec{c}\bigr\vert = \bigl\vert\vec{a}\bigr\vert\bigl\vert\vec{b}\bigr\vert\sin(\sphericalangle(\vec{a},\vec{b}))\, . $

\includegraphics[width=0.6\linewidth]{vektorprodukt_en.eps}

Alternatively, we have

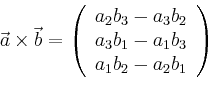
\begin{displaymath} \vec{a}\times\vec{b}=\left( \begin{array}{c} a_2 b_3 - a_... ..._3 b_1 - a_1 b_3 \\ a_1 b_2 - a_2 b_1 \end{array} \right) \end{displaymath}

In order to prove the equivalence of the two definitions, first, we show that both definitions are linear in both components, i.e. for the first component

$\displaystyle (\vec{a} + \vec{d}) \times \vec{b} = \vec{a} \times \vec{b} + \vec{d} \times \vec{b} $

and for an arbitrary $ \alpha \in \mathbb{R}$

$\displaystyle \alpha ( \vec{a} \times \vec{b} ) = (\alpha \vec{a}) \times \vec{b} .$

Similarly for the second component

$\displaystyle \vec{a} \times (\vec{b} + \vec{c}) = \vec{a} \times \vec{b} + \vec{a} \times \vec{c} $

and for an arbitrary $ \alpha \in \mathbb{R}$

$\displaystyle \alpha ( \vec{a} \times \vec{b} ) = \vec{a} \times ( \alpha \vec{b}) .$

For the definition of the vector product by coordinates this is a routine calculation. For the geometric definition only additivity is not evident.

To show this additivity we show

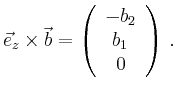
$\displaystyle \vec{e}_z\times \vec{b} = \left(\begin{array}{c}-b_2\\ b_1\\ 0\end{array}\right)\, . $

\includegraphics[width=0.5\linewidth,clip]{kreuzprodukt.eps}

As we can see in the figure, we obtain the vector product by projecting the vector $ \vec{b}$ onto the $ xy$-plane and then rotating this projection by angle $ \pi/2$ (this follows the right hand rule). Since the projection's length is

$\displaystyle \bigl\vert\vec{b}\bigr\vert \sin(\sphericalangle(\vec{e}_z,\vec{b})) $

we obtain the above formula.

Linearity in the second component follows now easily with this formula, because we may w. l. o. g. choose the coordinate system in such a way that $ \vec{e}_z$ coincides with the first vector. Similarly one shows the additivity of the geometric definition in the first component.

Now, it is sufficient to verify the equivalence of the definitions for all combinations of the canonical basis vectors $ \vec{e}_x$, $ \vec{e}_y$, $ \vec{e}_z$.

(temporary unavailable)
[previous page] [next page] [table of contents][page overview]
  automatically generated 10/30/2007