Mo logo [home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff] german flag
Mathematics-Online course: Basic Mathematics - Real Numbers

Normalized Floating Point Number

[previous page] [next page] [table of contents][page overview]

A $ p$-digit floating point number with base $ \beta$,

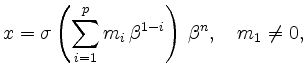
$\displaystyle x = \sigma \left( \sum _{i=1}^{p} m_i\,\beta^{1-i} \right)\,\beta^n, \quad m_1\neq 0, $

consists of a sign $ \sigma=\pm 1$, a mantissa $ m$ with $ m_i\in\{0,\ldots,\beta-1\}$, and an exponent $ n$ with $ n_{\text{min}}\leq n\leq n_{\text{max}}$.

The smallest and largest positive floating point numbers are

$\displaystyle x_{\min}=\beta^{n_{\text{min}}},\quad x_{\max}=\beta^{n_{\text{max}}+1}(1-\beta^{-p})\,. $

In particular, 0 does not have a floating point representation.

Besides the standard decimal representation ($ \beta=10$), dual ($ \beta=2$) and hexadecimal ($ \beta=16$) floating point numbers are frequently used.

[previous page] [next page] [table of contents][page overview]
  automatically generated 10/31/2008