Mo logo [home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff] german flag
Mathematics-Online course: Basic Mathematics - Real Numbers

Rational Numbers

[previous page] [next page] [table of contents][page overview]
The rational numbers consist of signed fractions of integers:

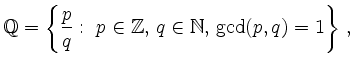
$\displaystyle {\mathbb{Q}} = \left\{\frac{p}{q}:\ p\in{\mathbb{Z}},\, q\in\mathbb{N},\, \operatorname{gcd}(p,q)=1 \right\} \,, $

where $ \operatorname{gcd}$ denotes the greatest common divisor. The set of rational numbers forms a field with the standard arithmetic operations (addition/subtravtion and multiplication/division).

As is illustrated in the figure, $ \mathbb{Q}$ is countable. With the so-called diagonal method, we can enumerate all positive fractions. Uncancelled fractions are skipped in the count.

Finally, the rational numbers form a dense subset of the real line. Between any two different rational numbers there are infinitely many rational numbers.

(Authors: Höllig/Kimmerle/Abele)
[previous page] [next page] [table of contents][page overview]
  automatically generated 10/31/2008