

Mathematics-Online course: Linear Algebra - Linear Systems of Equations - Approximation Problems

|
[home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff] |

|
|
Mathematics-Online course: Linear Algebra - Linear Systems of Equations - Approximation Problems | ||
Best Fitting Line | ||
| [previous page] [next page] | [table of contents][page overview] |
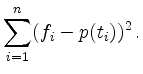
![\includegraphics[width=.7\moimagesize]{a_ausgleichsgerade}](/inhalt/aussage/aussage629/img5.png)
If we have at least two different ![]() -coordinates,
we obtain the following formulas
for the axis intercept
-coordinates,
we obtain the following formulas
for the axis intercept ![]() and the slope
and the slope ![]() :
:
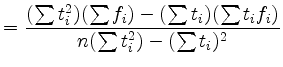 |
||
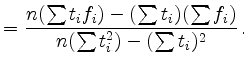 |
| automatically generated 4/21/2005 |