

Mathematics-Online lexicon: Annotation to

|
[home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff] |

|
|
Mathematics-Online lexicon: Annotation to | ||
Taylor Polynomial | ||
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z | overview |
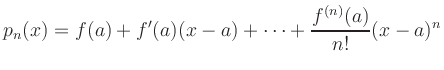
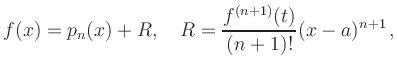
A straightforward computation shows that the derivatives of
![]() and
and ![]() match.
match.
To check the expression for the remainder ![]() , we augment an additional
term:
, we augment an additional
term:
| automatisch erstellt am 20. 7. 2016 |