Mo logo [home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff] german flag
Mathematics-Online lexicon: Annotation to

Absolute Value of Complex Numbers

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z overview

The absolute value of a complex number $ z=x+\mathrm{i}y$ is defined as

$\displaystyle \vert z\vert = \sqrt{x^2 + y^2} = \sqrt{z\bar z} . $

For $ z\in\mathbb{R}$ this definition is consistent with the definition of the absolute value of real numbers and has corresponding properties.

The positivity of the absolute value is straightforward; multiplicativity can easily be proved via the definition.

In order to prove the triangle inequality, we square the inequalities and subtract $ \vert z_1\vert^2 + \vert z_2\vert^2$. This yields

$\displaystyle -2\vert z_1\vert\vert z_2\vert \leq z_1 \bar z_2 + \bar z_1 z_2 \leq 2\vert z_1\vert\vert z_2\vert \,. $

These inequalities are equivalent to

$\displaystyle \mathrm{Re}(z_1 \bar z_2) \le \vert z_1\vert\vert z_2\vert \,, $

and therefore

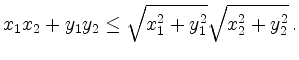
$\displaystyle x_1x_2 + y_1y_2 \le \sqrt{x_1^2+y_1^2} \sqrt{x_2^2+y_2^2} \,. $

Squaring again, we finally obtain

$\displaystyle 2x_1x_2y_1y_2 \leq x_1^2y_2^2 + x_2^2y_1^2 \,, $

which is correct in view of the non-negativity of $ (x_1y_2-x_2y_1)^2$.

(Authors: Kimmerle/Abele)
[Back]
  automatisch erstellt am 11.  6. 2007