

Mathematics-Online lexicon: Annotation to

|
[home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff] |

|
|
Mathematics-Online lexicon: Annotation to | ||
Vector Product | ||
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z | overview |
![\includegraphics[width=0.6\linewidth]{vektorprodukt_en.eps}](/inhalt/aussage/aussage445/img5.png)
Alternatively, we have
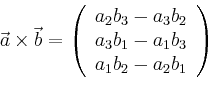
In order to prove the equivalence of the two definitions, first, we show that both definitions are linear in both components, i.e. for the first component
and for an arbitrary
![]()
Similarly for the second component
and for an arbitrary
![]()
For the definition of the vector product by coordinates this is a routine calculation. For the geometric definition only additivity is not evident.
To show this additivity we show
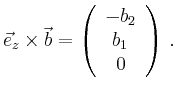
![\includegraphics[width=0.5\linewidth,clip]{kreuzprodukt.eps}](/inhalt/erlaeuterung/erlaeuterung210/img7.png)
As we can see in the figure, we obtain the vector product
by projecting the vector ![]() onto the
onto the ![]() -plane and then
rotating this projection by angle
-plane and then
rotating this projection by angle ![]() (this follows the right hand rule).
Since the projection's length is
(this follows the right hand rule).
Since the projection's length is
Linearity in the second component
follows now easily with this formula,
because we may w. l. o. g. choose the coordinate system in such a way that
![]() coincides with the first vector.
Similarly one shows the additivity of the geometric definition
in the first component.
coincides with the first vector.
Similarly one shows the additivity of the geometric definition
in the first component.
Now, it is sufficient to verify the equivalence of the definitions
for all combinations of the canonical basis vectors
![]() ,
,
![]() ,
,
![]() .
.
| automatisch erstellt am 17. 3. 2011 |