

Mathematik-Online lexicon:

|
[home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff] |

|
|
Mathematik-Online lexicon: | ||
Examples: Inproper Integral | ||
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z | overview |
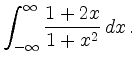
An antiderivative of the integrand is
The wrong approach
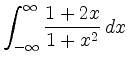 |
![$\displaystyle = \lim_{b\to\infty} \int_{-b}^{b} \frac{1+2x}{1+x^2}\,dx = \lim_{b\to\infty} \left[\arctan(x)+\ln(1+x^2)\right]_{-b}^{b}$](/inhalt/beispiel/beispiel991/img4.png) |
|
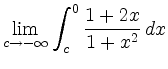 |
||
|
nor the limit
| ||
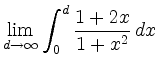 |
||
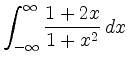
not exists.
see also:
| automatisch erstellt am 12. 9. 2008 |