Mo logo [home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff] german flag
Mathematik-Online lexicon:

Circuits

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z overview
Displaying statements as switches that are closed if the statement is true (and open if the statement is false, respectively), the and-connective can be represented by a serial connection and the or-connective by a parallel connection.
and-connective or-connective
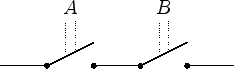\includegraphics{logische_schaltungen_und} \includegraphics[origin=tl]{logische_schaltungen_oder}

A negated statement corresponds to a switch that is closed if the statement is false. Thus it is possible to draw circuits representing equivalence, antivalence and implication.

Equivalence: $ A \Leftrightarrow B$ which can be rewritten as $ (A \land B) \lor (\lnot A \land \lnot B)$
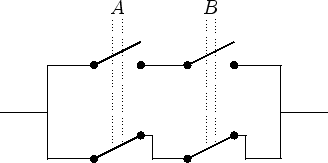\includegraphics{logische_schaltungen_gleich}
Antivalence: $ A \not\equiv B$ which can be rewritten as $ (A \land \lnot B) \lor (\lnot A \land B)$
\includegraphics[origin=tl]{logische_schaltungen_ungleich}
Implication: $ A \Rightarrow B$ which can be rewritten as $ \lnot A \lor B$
\includegraphics[origin=tl]{logische_schaltungen_implikation}

Switches can be represented by transistors, for example, that conduct electricity when a high or low voltage is impressed. Values w and f (or 1 and 0) represent high and low voltages respectively.

DIN 40900 defines symbols for the corresponding circuits. These consist of rectangles in which the respective operations are inscribed. Negation is symbolized by a circle.

Conjunction Disjunction Antivalence
\includegraphics[width=0.25\moimagesize]{din_und} \includegraphics[width=0.25\moimagesize]{din_oder} \includegraphics[width=0.25\moimagesize]{din_exor}
Negation Implication Equivalence
\includegraphics[width=0.25\moimagesize]{din_not} \includegraphics[width=0.25\moimagesize]{din_implikation} \includegraphics[width=0.25\moimagesize]{din_gleich}
(Authors: Hörner/Abele)

see also:

  automatisch erstellt am 11.  6. 2007