

Mathematik-Online lexicon:

|
[home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff] |

|
|
Mathematik-Online lexicon: | ||
Curve Sketching of a Rational Function | ||
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z | overview |
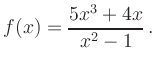
Symmetry: The numerator is even and the denominator is odd. Thus the function is odd, i.e., symmetric with respect to the origin.
Periodicity: The function is not periodic.
Points of Discontinuity and Poles:
The denominator of ![]() has simple zeros at
has simple zeros at ![]() .
Since the numerator is nonzero at these points, the singularities are not
removable and hence
.
Since the numerator is nonzero at these points, the singularities are not
removable and hence ![]() and
and ![]() are simple poles.
are simple poles.
Zeros:
The nominator vanishes at ![]() .
.
Extrema: The derivative
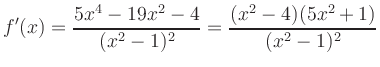
Inflection Points: The second derivative
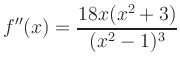
Asymptotes: Polynomial division yields
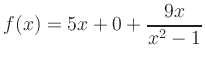
![\includegraphics[width=10.4cm]{Kurvendiskussion_2_en}](/inhalt/beispiel/beispiel46/img21.png)
see also:
| automatisch erstellt am 6. 12. 2016 |