Mo logo [home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff] german flag
Mathematik-Online lexicon:

Derivative

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z overview
To illustrate the dimension formula, let us consider the $ k$-th derivative on the space of polynomials of degree $ \le n$.

At first, let $ k=1$ and $ n=2$. For the space of polynomials of degree $ \le 2$ the monomials $ \{1,x,x^2\}$ form a basis. Hence, the space has the dimension 3.

For $ p(x)=a_0+a_1x+a_2x^2$ the polynomial $ p'(x)=a_1+2a_2x$ has degree $ \le 1$. Thus, the image space has dimension 2.

The derivative of a constant vanishes, and the constants form a one-dimensional subspace. Hence, the kernel of the mapping has dimension 1 and the dimension formula is satisfied by $ 3=1+2$.

In general a polynomial has the form

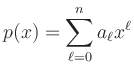
$\displaystyle p(x)=\sum_{\ell =0}^n a_\ell x^\ell $

and its $ k$-th derivative has the form

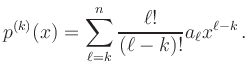
$\displaystyle p^{(k)}(x)=\sum_{\ell =k}^n \frac{\ell !}{(\ell -k)!}a_\ell x^{\ell -k}\,. $

Hence, the image is a polynomial of degree $ \le n-k$ and polynomials of degree $ <k$ are nullified. Thus, the dimension formula reads as follows:

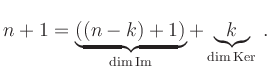
$\displaystyle n+1=\underbrace{((n-k)+1)}_{\dim \operatorname{Im}} + \underbrace{k}_{\dim \operatorname{Ker}}\,. $

see also:

  automatisch erstellt am 25.  6. 2018