Mo logo [home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff] german flag
Mathematik-Online lexicon:

Taylor Polynomial of the Sine Function

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z overview
The derivatives of the sine function $ f(x) = \sin{x}$ are

$\displaystyle f^{{\prime}} = \cos{x},\quad f^{{\prime}{\prime}} = -\sin{x},\quad f^{{\prime}{\prime}{\prime}} = -\cos{x},\quad f^{(4)} = f = \sin{x}, ... \,. $

With the values

$\displaystyle f^{{\prime}}(0) = 1,\quad f^{{\prime}{\prime}}(0) = 0,\quad f^{{\prime}{\prime}{\prime}}(0) = -1,\quad f^{(4)}(0) = f = 0, ... \,, $

we obtain the first few taylor polynomials:

$\displaystyle p_1(x)$ $\displaystyle = x$    
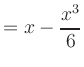$\displaystyle p_3(x)$ $\displaystyle = x -\frac{x^3}{6}$    
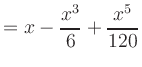$\displaystyle p_5(x)$ $\displaystyle = x -\frac{x^3}{6} + \frac{x^5}{120}$    
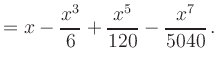$\displaystyle p_7(x)$ $\displaystyle = x -\frac{x^3}{6} + \frac{x^5}{120} - \frac{x^7}{5040} \,.$    

Similarly, the Taylor polynomials of the cosine function up to degree $ 6$ are

$\displaystyle p_0(x)$ $\displaystyle = 1$    
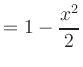$\displaystyle p_2(x)$ $\displaystyle = 1 - \frac{x^2}{2}$    
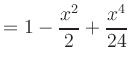$\displaystyle p_4(x)$ $\displaystyle = 1 - \frac{x^2}{2} + \frac{x^4}{24}$    
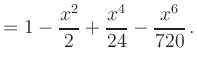$\displaystyle p_6(x)$ $\displaystyle = 1 - \frac{x^2}{2} + \frac{x^4}{24} - \frac{x^6}{720}\,.$    

The approximations are very accurate for small $ x$. For example, we can bound the error of the approximation

$\displaystyle \sin{0.1} \approx p_{4}(0.1) = 0.09983... $

by

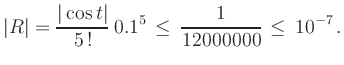
$\displaystyle \vert R\vert = \frac{\vert\cos{t}\vert}{5\,!}\,0.1^5 \, \leq \, \frac{1}{12000000} \, \leq \, 10^{-7}\,. $

\includegraphics[height=4.5cm]{Taylor_sin}   \includegraphics[height=4.5cm]{Taylor_cos}

As illustrated by the figure, for large $ x$, the approximation becomes sufficiently accurate only for higher degree. The table shows the errors for several $ x$.

$ x$ $ \pi$ $ \pi/2$ $ \pi/3$ $ \pi/4$ $ \pi/5$ $ \pi/6$
$ p_1(x)$ 3.1416 0.5708 0.1812 0.0783 0.0405 0.0236
$ p_3(x)$ 2.0261 0.0752 0.0102 0.0025 0.0008 0.0003
$ p_5(x)$ 0.5240 0.0045 0.0003 0.0000 0.0000 0.0000
$ p_7(x)$ 0.0752 0.0002 0.0000 0.0000 0.0000 0.0000
$ p_0(x)$ 2.0000 1.0000 0.5000 0.2929 0.1910 0.1340
$ p_2(x)$ 2.9348 0.2337 0.0483 0.0155 0.0064 0.0031
$ p_4(x)$ 1.1239 0.0200 0.0018 0.0003 0.0001 0.0000
$ p_6(x)$ 0.2114 0.0009 0.0000 0.0000 0.0000 0.0000

see also:

  automatisch erstellt am 20.  7. 2016