Mathematics-Online lexicon: Stokes Theorem

	[home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff]
	Mathematics-Online lexicon:
	Stokes Theorem

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

overview

Let be a bounded orientable surface parametrized by $\sigma (t,u)$ with normal vector $N(t,u) = \sigma_t \times \sigma_u .$ Define the top side of as this side where points outward. Assume that the boundary $\partial S$ is parametrized in such a way that the top side of lies on the left and assume that $\partial S$ consists of finitely many smooth curves.

Then for each continuous differentiable vector field $\Phi$ defined on an open set containing and its boundary

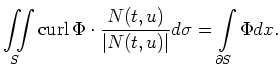
$\displaystyle \iint\limits_S \operatorname{curl} \Phi \cdot \frac{N(t,u)}{\vert N(t,u)\vert} d\sigma = \int\limits_{\partial S} \Phi dx .$

The theorem of Stokes expresses the flux of the curl of $\Phi$ through as the curve integral of $\Phi$ along the boundary of The special case when is contained in the - plane is known as Green's theorem.

The theorem does not apply to non-orientable surfaces. A Moebius strip is an example for a non-orientable surface in $\mathbb{R}$ ^3.

()

Examples:

Beispiel: Satz von Stokes (german)
Satz von Stokes bei einer kreisförmigen Strömung (german)

[Annotations] [Links]

automatically generated 7/ 4/2005