

Mathematics-Online lexicon:

|
[home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff] |

|
|
Mathematics-Online lexicon: | ||
Greens Theorem | ||
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z | overview |
Green's theorem may be considered as a special case of the integral theorem of Stokes in space.
Standard Version.
Let ![]() and
and ![]() be continuous differentiable functions on a region
be continuous differentiable functions on a region ![]() which is the interior
of a closed path
which is the interior
of a closed path ![]() . Suppose that
. Suppose that ![]() is parametrized counterclockwise and
let
is parametrized counterclockwise and
let
![]() Then
Then
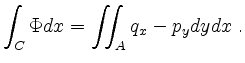
General Version.
Let ![]() be a region in the plane whose boundary consists of a finite number of
smooth curves
be a region in the plane whose boundary consists of a finite number of
smooth curves
![]() . Assume that each curve
. Assume that each curve ![]() of the
is parametrized by
of the
is parametrized by
![]() in such
a way
that
in such
a way
that ![]() lies to the left of the curve.
Let
lies to the left of the curve.
Let
![]() be a continuous differentiable vector
field.
be a continuous differentiable vector
field.
Then
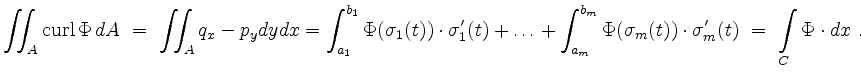
Note that in the general version the boundary curves need not form a closed path.
Green's theorem expresses the curve integral of a vector field as a double integral over its scalar curl. Sometimes the calculation of the double integral is easier than that one of the curve integral and vice versa.
see also:
| automatically generated 6/ 2/2008 |