Mo logo [home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff] german flag
Mathematics-Online lexicon:

Line Integral

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z overview

Let $ \sigma: [a,b] \longrightarrow \mathbb{R}^n $ be a regular parametric curve $ C$ and let $ \Phi: \mathbb{R}^n \longrightarrow \mathbb{R}^n $ be a differentiable vector field defined on open set containing $ C .$

Then the integral

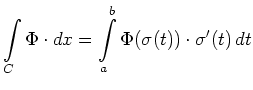
$\displaystyle \int\limits_C \Phi \cdot dx =\int\limits_a^b \Phi (\sigma(t)) \cdot \sigma'(t) \,dt $

is called the line integral (often also called curve integral) of the vector field $ \Phi $ along $ C .$

\includegraphics[width=.5\linewidth]{a_arbeitsintegral_bild}

For parametrizations of $ C$ with the same orientation the line integrals has the same value. If the curve is traversed in the oppposite direction then the line integral changes its sign.

For $ \Phi (x,y,z) = (p(x,y,z), q(x,y,z), r(x,y,z)) $ the line integral is often written in the form

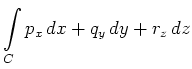
$\displaystyle \int\limits_C p_x\,dx + q_y\,dy+r_z\,dz $

with $ dx=x'(t)\,dt\,,\,dy=y'(t)\,dt\,,\, dz=z'(t)\,dt$.

The conditions on the smoothness of $ \Phi $ and $ \sigma $ may be weakened. For example it suffice that $ \sigma $ is regular except at a finite number of points.

Physical Interpretation: the vector field may be interpreted as force field. The line integral represents the work done by (or against) this force along the curve $ C$ (from $ \sigma (a)$ till $ \sigma (b)$ ). The work may depend on the path, i.e. if different paths are taken between the endpoints the work may be different. The force field may be given by electrostatical or gravitational attraction.

()

see also:

[Annotations] [Examples]
  automatically generated 7/ 5/2005