Mo logo [home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff] german flag
Mathematics-Online lexicon:

Directional Derivative

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z overview
The directional derivative, i.e. the derivative in direction of a vector $ v$, is given as

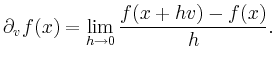
$\displaystyle \partial_v f(x) = \lim_{h\to0} \frac{f(x+hv)-f(x)}{h} . $

With the chain rule it may be calculated as

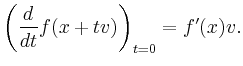
$\displaystyle \left(\frac{d}{dt} f(x+tv)\right)_{t=0} = f^\prime(x)v . $

Especially $ \partial_{e_\nu} f$ coincides with the $ \nu $-th partial derivative.

The directional derivative is the rate of change of $ f$ along the straight line through $ x$ in direction $ v .$ It is maximal when $ v$ has the same direction as    grad$ \,f(x)$ and least when $ v$ points in the opposite direction.

\includegraphics[width=.65\moimagesize]{Richtungsabl_Bild}

()

Examples:

[Links]
  automatically generated 5/30/2011