Mo logo [home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff] german flag
Mathematics-Online lexicon:

Multivariate Function

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z overview

A multivariate real function (often also called a real function of several variables) is a map

$\displaystyle f:\mathbb{R}^n \supseteq D \to\mathbb{R}^m,\quad x\mapsto f(x)\, . $

$ D$ is called the domain of definition. $ f = f(x_1, \ldots, x_n)$ assigns to each vector $ x = (x_1,\ldots,x_n)^{\operatorname t}\in D$ a vector $ (f_1(x),\ldots,f_m(x))^{\operatorname t}\in \mathbb{R}^m .$. So $ f$ depends on $ n$ variables $ x_1, \ldots ,x_n .$

If $ n,m \le 3$ the variables are often denoted by $ x, y$ and $ z$ (accordingly to the coordinate axes). E.g. one writes for $ m=n=2$

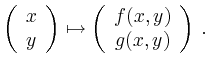
$\displaystyle \left(\begin{array}{c}x\\ y\end{array}\right) \mapsto \left(\begin{array}{c}f(x,y)\\ g(x,y)\end{array} \right) \,. $

$ f$ is called a scalar function, if $ (m=1) .$

If $ n=1$ (and $ f$ is continuous), then $ f$ is called a parametrized curve.

If $ m \geq 2$ then $ f$ is called a vector field. The values of $ f$ are in this case vectors and no scalars.

Examples:

[Links]
  automatically generated 5/26/2011