Mo logo [home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff] german flag
Mathematics-Online lexicon:

Higher Partial Derivatives

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z overview
Since partial derivatives are themselves functions, we can repeat the process of partial differentiation.

Second partial derivatives are denoted by

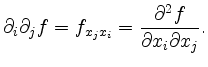
$\displaystyle \partial_i \partial_j f = f_{x_jx_i} = \frac{\partial^2 f}{\partial x_i \partial x_j} .$

Similarly higher partial derivatives are written $ \partial_i\partial_j\partial_k\ldots f .$

In the case when mixed partial derivatives are equal (i.e. it does not matter whether the partial derivatives are taken first with respect to a variable $ x_i$ and then with respect to $ x_j$ or vice versa) one can use multiindices for higher partial derivatives.

$\displaystyle \partial^\alpha f = \partial_1^{\alpha_1}\cdots\partial_n^{\alpha_n} f, \quad \alpha=(\alpha_1,\ldots,\alpha_n)\, , $

Here the index $ \alpha_i \in \mathbb{N}_0$ denotes the number of partial derivatives with respect to the $ i$-th variable. The sum $ \left\vert \alpha \right\vert=\alpha_1+\cdots +\alpha_n$ is called the order of the partial derivative.

()
[Examples] [Links]
  automatically generated 8/ 4/2008