Mo logo [home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff] german flag
Mathematics-Online lexicon:

Orthogonal Basis

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z overview
An orthonormal basis consists of $ 3$ mutually orthogonal unit vectors $ \vec{u}$, $ \vec{v}$, $ \vec{w}$.

\includegraphics[width=.7\linewidth]{a_on_basis}

As illustrated in the figure, any vector $ \vec{a}$ can be represented by a linear combination

$\displaystyle \vec{a} = (\vec{a}\cdot\vec{u})\vec{u} + (\vec{a}\cdot\vec{v})\vec{v} + (\vec{a}\cdot\vec{w})\vec{w}\,. $

The addends are the projections of $ \vec{a}$ onto the axes generated by the vectors of the ONB. For the coefficients we have

$\displaystyle \left\vert\vec{a}\cdot\vec{u}\right\vert^2+\left\vert\vec{a}\cdot... ...t^2+\left\vert\vec{a}\cdot\vec{w}\right\vert^2=\left\vert\vec{a}\right\vert^2. $

In particular, we have

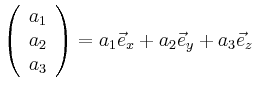
$\displaystyle \left(\begin{array}{c}a_1\\ a_2\\ a_3\end{array}\right) = a_1 \vec{e}_x + a_2 \vec{e}_y + a_3 \vec{e}_z $

for the canonical orthonormal basis of the Cartesian coordinate system

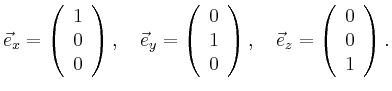
$\displaystyle \vec{e}_x = \left(\begin{array}{c}1\\ 0\\ 0\end{array}\right),\qu... ...\right),\quad \vec{e}_z = \left(\begin{array}{c}0\\ 0\\ 1\end{array}\right). $

see also:

[Annotations] [Examples]
  automatically generated 3/17/2011