Mathematics-Online lexicon: Trapezoid Rule

	[home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff]
	Mathematics-Online lexicon:
	Trapezoid Rule

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

The approximation

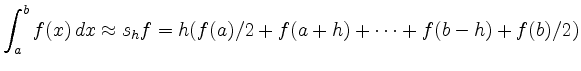
$\displaystyle \int_a^b f(x)\, dx \approx s_h f = h (f(a)/2 + f(a+h) + \cdots + f(b-h) + f(b)/2)$

refers to the integral as a sum of trapezoids.

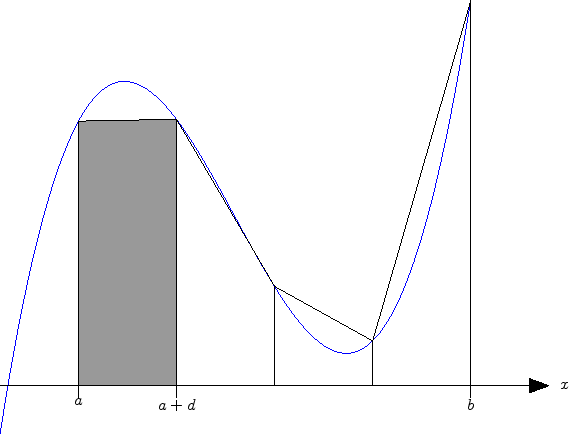
$\includegraphics{trapez2.eps}$

For a twice continuously differentiable function, the error can be estimated via

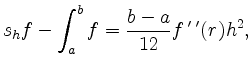
$\displaystyle s_h f - \int_a^b f = \frac{b-a}{12} f\,'\,'(r) h^2,$

with $r\in[a,b]$ .

More precisely, the error for smooth functions bears the asymptotic expansion

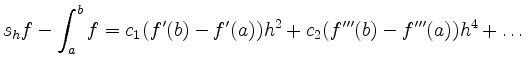
$\displaystyle s_h f - \int_a^b f = c_1(f^\prime(b)-f^\prime(a))h^2 + c_2(f^{\prime\prime\prime}(b)-f^{\prime\prime\prime}(a)) h^4 + \dots$

with constants

independent from

and

. Thus the trapezoid rule is very exact for

-periodic functions. The error strives faster towards zero than any

-potence.

(Authors: Höllig/Hörner/Abele)

Example:

automatically generated 4/ 7/2008