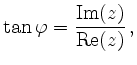Complex numbers
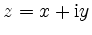 can be identified with the points
of the real plane. Their absolute value corresponds to their
distance from the origin, while their real and imaginary parts are their projections onto the real and imaginary axes
respectively.
The complex conjugate of a complex number is obtained
by reflection with respect to the real axis.
can be identified with the points
of the real plane. Their absolute value corresponds to their
distance from the origin, while their real and imaginary parts are their projections onto the real and imaginary axes
respectively.
The complex conjugate of a complex number is obtained
by reflection with respect to the real axis.
In polar coordinates, the Euler-Moivre-formula yields the
representation
with 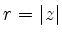 .
The angle
.
The angle 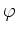 is determined only up to
multiples of
is determined only up to
multiples of 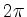 ;
it is called the argument of
;
it is called the argument of 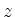 :
It is common practice to use
:
It is common practice to use
![$ (-\pi,\pi]$](/inhalt/aussage/aussage378/img10.png) as the standard interval
(principal value).
Moreover,
i.e., the argument
as the standard interval
(principal value).
Moreover,
i.e., the argument
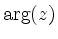 can
be determined from the quotient
can
be determined from the quotient 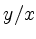 .
However, one has to select the correct branch.
If
.
However, one has to select the correct branch.
If
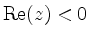 ,
,
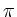 or
or 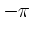 must be added
to the inverse function's value.
must be added
to the inverse function's value.
In the table below some complex numbers are given in polar
coordinates.
(Authors: Höllig/Kopf/Abele)
Example:
| |
automatically generated
6/11/2007 |




![\includegraphics[width=0.4\moimagesize]{a_gausssche_bild1}](/inhalt/aussage/aussage378/img2.png)
![\includegraphics[width=0.4\moimagesize]{a_gausssche_bild2}](/inhalt/aussage/aussage378/img3.png)