The simplex algorithm for solving a linear program
updates an admissible basic solution 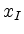 with successive
pivot operations until an optimal vector
with successive
pivot operations until an optimal vector 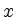 is reached.
One step
which utilizes the simplex tableau
is reached.
One step
which utilizes the simplex tableau
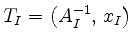 , has the following form:
, has the following form:
(i) First, with 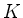 , the complementary set to
, the complementary set to 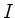 ,
one computes
,
one computes
and defines 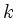 as the smallest index, where
as the smallest index, where 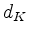 attains
its minimum. If
attains
its minimum. If
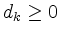 , the current basic solution
, the current basic solution 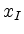 is optimal and the algorithm terminates.
is optimal and the algorithm terminates.
(ii) If the auxiliary vector
is 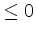 , the infimum of the cost function is
, the infimum of the cost function is 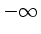 and the
linear program has no solution. Otherwise,
and the
linear program has no solution. Otherwise, 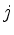 is the smallest index,
for which the quotients
are minimal.
is the smallest index,
for which the quotients
are minimal.
(iii) The tableau 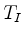 is updated,
is updated,
by
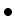
- dividing the row with index
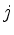 by
by 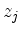 ,
,
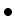
- subtracting, for each
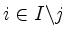 ,
from the row with index
,
from the row with index 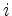 the modified row with index
the modified row with index 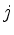 multiplied by
multiplied by 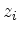 .
.
(Authors: Höllig/Pfeil/Walter)
| |
automatically generated
4/24/2007 |




![]() , the complementary set to
, the complementary set to ![]() ,
one computes
,
one computes
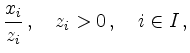
![]() is updated,
is updated,