Mathematics-Online lexicon: Linear Program

	[home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff]
	Mathematics-Online lexicon:
	Linear Program

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

A linear program is an optimization problem with linear cost function,

$\displaystyle c^{\operatorname t} x\longrightarrow \min \,,$

equality constraints and non-negative unknowns

$\displaystyle Ax=b \,, \quad x \geq 0 \,.$

Usually, it is assumed that the 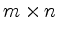$m \times n$ matrix

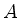has full rank 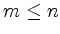$m \leq n$ . This can always be achieved by removing redundant constraints.

General linear constraints

$\displaystyle P y = q \,, \quad R y \leq s$

for unknowns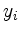

can be brought into the above standard form by introducing auxiliary variables. We write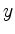

as the difference of two non-negative vectors,

$\displaystyle y=u-v \,, \quad u \geq 0 \,, \; v \geq 0 \,,$

and introduce non-negative slack variables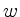

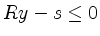to remove the inequality constraints. More precisely, $Ry-s \leq 0$ is replaced by

$\displaystyle Ry -s+w =0 \,, \quad w \geq 0 \,,$

where

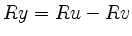(Authors: Höllig/Pfeil/Walter)

Example:

automatically generated 4/24/2007