Mo logo [home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff] german flag
Mathematics-Online lexicon:

Loss of significant digits

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z overview

The absolute relative error of a floating point addition can be estimated by

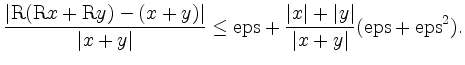
$\displaystyle \frac{\vert\text{R}(\text{R}x+\text{R}y)-(x+y)\vert}{\vert x+y\ve... ...}+\frac{\vert x\vert+\vert y\vert}{\vert x+y\vert}(\text{eps}+\text{eps} ^2). $

For summands of the same sign, the right-hand side is $ \leq 2$eps$ +O($eps$ ^2)$. On the other hand, if $ y\approx -x$, the quotient $ (\vert x\vert+\vert y\vert)/\vert x+y\vert$ becomes very large. If the first $ s$ digits of $ x$ and $ y$ with respect to the base $ \beta$ coincide, the relative error can be

$\displaystyle > 2\beta^{s-1}$eps$\displaystyle . $

The leading digits cancel when forming the difference, potentially causing a large error, since the difference is represented by fewer accurate digits.

Annotation:

[Examples] [Links]
  automatically generated 7/25/2011