Mathematics-Online lexicon: Linear Systems of Equations in Two Variables

	[home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff]
	Mathematics-Online lexicon:
	Linear Systems of Equations in Two Variables

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

overview

A linear system of equations in two unknowns ("variables")

and

has the form

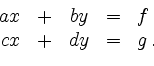
$\begin{displaymath} \begin{array}{rcrcl} ax & + & by &=& f \\ cx & + & dy &=& g\,. \end{array}\end{displaymath}$

The system has a unique solution for all

, iff

$\displaystyle \Delta = ad-bc\neq 0\,.$

The solution

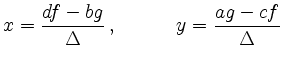
$\displaystyle x=\frac{df-bg}{\Delta}\,,\qquad\quad y=\frac{ag-cf}{\Delta}$

can be interpreted as the intersection of the lines given by the two equations.

$\includegraphics[width=6cm]{lgsgeraden}$

If $\Delta=0$ , the lines are parallel to one another. In this case either no solution exists or - if the lines coincide - there are infinitely many solutions.

(Authors: Höllig/Abele)

see also:

Keyword: System of equations, linear

[Examples]

automatically generated 9/18/2007