Mo logo [home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff] german flag
Mathematics-Online lexicon:

Parameter Integrals and Iterated Integrals

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z overview

Let $ f = f(x_1, \ldots , x_n)$ be a continuous real scalar function. Fix an index $ i .$ An integral of the form

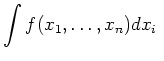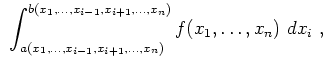
$\displaystyle \int f(x_1, \ldots , x_n) dx_i \ $   or$\displaystyle \ \int_{a(x_1, \ldots ,x_{i-1}, x_{i+1}, \ldots ,x_n)}^{b(x_1, \ldots ,x_{i-1}, x_{i+1}, \ldots ,x_n)} f(x_1, \ldots , x_n) \ dx_i \ ,$

where all variables $ x_j$ with $ j \neq i$ are regarded as constants is called a parameter integral (the constant variables are its parameters). Such integrals may be seen as inverse operation to the partial differentiation with respect to $ x_i .$

An iterated integral is a sequence of parameter integrals of the following form.

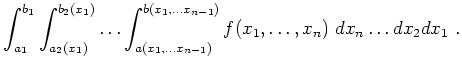
$\displaystyle \int_{a_1}^{b_1} \int_{a_2(x_1)}^{b_2(x_1)} \ldots \int_{a(x_1,... ...})}^{b(x_1, \ldots x_{n-1})} f(x_1, \ldots , x_n) \ dx_n \ldots dx_2 dx_1 \ .$

It is evaluated from the inside out. Iterated integrals may analogously be defined for each ordering of the variables.

()

see also:

  automatically generated 6/ 1/2005